Fibonacci sayılarını bulmanın bir başka yönteminden bahsedeceğiz. Bu yöntemi anlatmadan evvel öz yinelemeli bir dizinin karakteristik denklemini nasıl buluruz ona değinelim. Bilindiği gibi fibonacci sayı dizisi öz yinelemeli bir sayı dizisidir. Yani kendinden evvel ki sayılarla işlem yapılıp kendisi bulunan sayı dizileri öz yinelemelidir.
Fibonacci sayı dizisi; F(n)=F(n-1)+F(n-2) şeklinde ifade edilir. Kendinden önce gelen 2 sayının toplamı bir sonraki sayıyı verecek şekilde dizi ilerletilir.
Genelleştirilmiş bir fibonacci tanımı yapacak olursak;
F(n)=c*r^n olacak şekilde denklemi yeniden yazalım;
Denklemin her iki tarafını c*r^(n-2)’ ye bölersek sonuç şu şekilde olacaktır;
Bilindiği gibi fibonacci sayı dizisi için c katsayıları 1 dir. Bu durumda fibonacci sayı dizisinin karakteristik denklemini şu şekilde ifade etmek gerekir;
Bu karakteristik denklemin köklerine bakacak olursak;
elde etmiş oluruz. Peki ama bu kökler bizim ne işimize yarayacak?
Fransız matematikçi Binet ilk kez 1843 yılında fibonacci sayı dizisi için Binet formüllerini vermiştir. Ispatına burada girmeyeceğim.
∀n > 0 doğal sayısı için;
şeklinde bir bağıntı verir bize. Burada Φ ve Ψ bizim karakteristik denklemimizin köklerini ifade etmektedir. Bu durumda Binet denkleminin fibonacci sayı dizisi için özelleşmiş hali şu şekilde yazılabilir;
Bu bağıntı ile istediğimiz fibonacci sayısını bulabiliriz. Bir deneme yapalım. Örneğin; n = 14 olsun. Yani 14. fibonacci sayısını bulmak isteyelim. Denklemde n gördüğümüz yere 14 yazarsak sonucun 377 çıktığını görürüz. Gerçekten de 14. fibonacci sayısı 377 dir. Öyle mi?
1 1 2 3 5 8 13 21 34 55 89 144 233 377
Peki bu bağıntı ile yeni bir algoritma yazalım ve test edelim. Bakalım ne kadar hızlı.
Flowgorithm uygulaması ile bu chartı test edebilirsiniz.
Ayrıca programın tamamını da buradan indirebilirsiniz.
Aşağıda ki python kodlarına da bakalım.
Kod Bloğum:
import numpy as np
from timeit import default_timer as timer
st = timer()
alfa = (1 + np.sqrt(5)) / 2
beta = (1 - np.sqrt(5)) / 2
n = 85
Fn = int((np.power(alfa, n) - np.power(beta, n)) / (alfa - beta))
et = timer()
print(et - st)
print(" ")
print(Fn)
print(" ")
n=85 için çıkan sonuç 0,00019740000061574392 saniye. Bu değer oldukça iyi.
Daha büyük fibonacci sayıları için denemeler yapabilirsiniz.
Kolay gele…
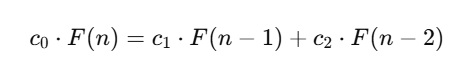
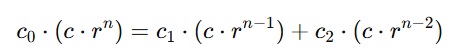
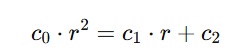
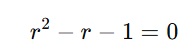
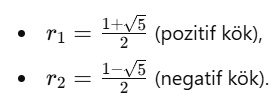
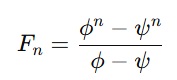
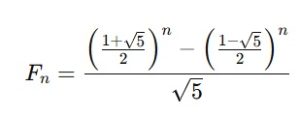
İlk Yorumu Siz Yapın